În prima parte a Evului Mediu vest-european izbînzile matematice ale lumii clasice greco-romane căzuseră în uitare; putem vedea aceasta răsfoind Etimologiile lui Isidor din Sevilla (c. 560-636), acest bestseller medieval, care putea fi găsit în atît de multe biblioteci ale acelei ere. Atunci cînd descrie ce e matematica, Isidor păstrează arhitectura descrisă de Platon cu secole înainte: matematica se compune din aritmetică, geometrie, astronomie și muzică. Și cît de redusă este descrierea aritmeticii în tratamentul lui Isidor! Odată cu nefolosirea și apoi uitarea limbii eline în peninsula iberică sub domnia vizigotă, întreaga abilitate de a calcula părea pierdută, simplele operații contabile se învecinau cu misterul. Oceanul uitării de cîteva veacuri va fi depășit grație unei recuperări influențate esențial de civilizația arabă, care avea să aducă nu doar un suflu inovator, ci și un nou sistem de numerație. În marele tablou al dezvoltării domeniului, două volume se dovedesc a fi fost cu adevărat importante: Liber mahamaleth, scrisă în jur de 1150 în Spania de Johannes Hispalensis, și Liber abaci, scrisă în jur de anul 1200 de Leonardo Fibonacci.
Dar aceste dezvoltări au fost precedate de adoptarea sistemului de numerație arab, un act care a beneficiat de intervenția salvatoare a unui matematician neobișnuit. Poate părea surprinzător: în vremurile cele mai întunecate ale Evului Mediu vest-european, Biserica Catolică a reprezentat un bastion al culturii și inovației. În mediul intelectual al lumii catolice, Gerbert d’Aurillac (c. 945-1003) s-a ridicat pînă la demnitatea de Papă, rămînînd în istorie drept Silvestru al II-lea, care s-a așezat în jilțul Sfîntului Petru din 999 și pînă la moartea sa. El a fost matematicianul care a folosit prima oară în Vestul creștin al Europei cifrele arabe și a avut și autoritatea de a recomanda și altora un fel de a calcula mai eficient, exact acel temei pe care s-a înălțat ulterior matematica Vestului. De aceea interesantă ni se pare perioada formativă a lui Gerbert. Părinții săi l-au încredințat unei abații benedictine. Acolo, Gerbert a devenit elevul unui călugăr pe nume Raimund, care i-a deschis drumul spre universul culturii, așa încît atunci cînd a avut ocazia să călătorească în Spania maură sub porunca contelui Borrell al II-lea al Barcelonei, a urmat nu doar o aventură geografică, ci și o transformare culturală profundă. Educația lui Gerbert a continuat întîi la Barcelona, apoi la Sevilla și Granada, care pe atunci erau importante centre multiculturale. (Povestea e spusă minunat de Nancy Marie Brown, în volumul The Abacus and the Cross: The Story of the Pope Who Brought the Light of Science to the Dark Ages [Basic Books, 2010].)
Acesta e contextul în care Gerbert d’Aurillac a devenit profund familiarizat cu folosirea sistemului decimal și a cifrelor arabo-indiene, deopotrivă cu folosirea abacului, lipsit în acea perioadă de folosirea cifrei zero. În loc de zero, se lăsa un spațiu liber. Întrebarea care-l preocupa pe Gerbert pe atunci era: cum se poate calcula repede și corect? Dacă e să credem o mărturie din veacul al XII-lea, Gerbert a deprins taina abacului de la un matematician din Fes, de la Universitatea al-Qarawiyyin, și folosirea sistemului zecimal părea să fie răspunsul la întrebare. Abacul lui Gerbert ar fi avut 27 de părți cu 9 simboluri numerice, care reprezentau cifrele, și o coloană liberă, care ar fi reprezentat cifra zero. Această mașinărie de calcul avea 1.000 de caractere, cioplite din corn de un magistru din Rheims. Mai tîrziu, cînd Gerbert a avut la rîndul lui elevi, unul dintre aceștia, Richer, ne-a lăsat o mărturie credibilă, că Gerbert putea performa grație abacului calcule extrem de sofisticate, pe atunci inaccesibile celor care se încăpățînau să utilizeze sistemul de numerație roman. Un alt elev al lui Gerbert, Bernelinus din Paris, avea să scrie un manual intitulat Liber abaci (cartea sa e diferită de opul lui Fibonacci), în care se descrie folosirea abacului lui Gerbert.
Cum de a fost posibil ca Gerbert să introducă o formă de calcul atît de eficientă în Europa ce ieșea din erele întunecate? În anul 969, contele Borrell al II-lea a călătorit la Roma și l-a luat cu el și pe Gerbert, prilej cu care tînărul învățat a fost prezentat Papei Ioan al XIII-lea și împăratului Otto I (al imperiului romano-german), care l-a angajat ca profesor al fiului său, viitorul împărat Otto al II-lea. Bătăliile politice de culise din perioada respectivă erau de o acerbie pe care azi abia de ne-o putem imagina, și e plauzibil că acestea au solicitat mult din energia creativă a viitorului papă. Rolul lui în istoria științelor rămîne mare, pentru că după secolul al XI-lea adepții sistemului de numerație decimal nu aveau decît să crească. Moștenirea Papei Silvestru al II-lea include volumul 139 din Patrologia Latină, conținînd un moment important al istoriei matematicii, și anume lucrările: Libellus de numerorum divisione; De geometria; Regula de abaco computi; Liber abaci; Libellus de rationali et ratione uti. Nu avem de-a face cu lucrări de cercetare, ci de expunere și popularizare, de familiarizare a publicului (ecleziastic și nu numai) cu un format de calcul accesibil și eficient. Cîteva dintre dezvoltările ulterioare ale matematicilor sînt masiv îndatorate acestei transformări a aritmeticii, iar povestea merită urmărită și în veacurile următoare, deși departe e de noi speranța de a o putea acoperi complet.
Multe dintre dezvoltările formalismului algebric de mai tîrziu sînt îndatorate lui François Viète (1540-1603), a cărui nouă algebră s-a dovedit a fi un punct de turnură important în dezvoltarea algebrei polinoamelor și în studiul ecuațiilor algebrice (al căror studiu avea să culmineze cu cercetările lui Niels Abel și Évariste Galois, la începutul secolului al XIX-lea). Să nu omitem a menționa că François Viète a fost consilier personal al regelui Henri de Navarra, pentru care a descifrat în 1590 codurile secrete ale Ligii catolice, ca un fel de Alan Turing al Renașterii. Dar contribuțiile lui importante în domeniul algebrei sînt formula binomială și legătura dintre rădăcinile unui polinom și coeficienții săi. Algebra înainte de François Viète era mult concentrată pe aplicațiile ei în finanțe, așa cum chestiunea era înțeleasă la finele Evului Mediu. Să chemăm spre mărturie un manuscris foarte interesant, scris și păstrat în limba occitană din veacul al XV-lea, Aritmetica de la Pamiers, aflat în posesia Bibliotecii Naționale din Paris și care conține o adevărată minune: e cel mai vechi manuscris care recunoaște un număr negativ ca soluție a unei probleme. Nu știm cu certitudine cine este autorul acestui tratat, redactat cel mai probabil în deceniul 1430, dar există o bănuială: Jean de Tolosa, perfect capabil să poarte căile algebrei spre un nivel mai înalt de tehnicalitate și utilitate. Unele dintre problemele curente bine ilustrate în acest volum e cea a convertirii unor monede dintr-una într-alta, precum și a unor măsuri dintr-una în cealaltă. Pe atunci, livrele din Montpellier nu erau egale cu cele din Avignon (era cu trei veacuri și jumătate înainte de introducerea sistemului metric). Ce coșmar ar fi fost aceste calcule în absența sistemului zecimal!
Dar, pentru a completa tabloul dezvoltării sistemului zecimal pe baza cifrelor numite azi arabe, nu am putea omite să amintim chestiunea virgulei zecimale (așa cum se folosește azi în română). Prima utilizare a separării în sistemul bazat pe cifre e din anul 952, și aparține lui Abu’l-Hasan al-Uqlidisi, într-un volum intitulat Capitole ale aritmeticii indiene. În Evul Mediu european, pentru a scrie 3,14, ar fi fost nevoie de o bară deasupra cifrei 3, astfel încît cititorul să înțeleagă că partea întreagă se oprește acolo. Alte notații propuse includ așa-numita separatrix, o bară verticală ce despărțea partea întreagă de partea zecimală. Notația cu punct după partea întreagă a fost popularizată de John Napier (1550-1617), creatorul logaritmilor (în volumul Mirifici Logarithmorum Canonis Descriptio, din 1614), care ne-a lăsat ca unealtă de calcul tabelul clasic de logaritmi, precum și combinația dintre logaritmii în baza naturală și funcțiile trigonometrice, o contribuție atît de importantă în dezvoltarea tehnicilor de calcul. Nu a fost deloc ușor la vremea respectivă să se descopere baza în care se calculează logaritmii naturali, și anume numărul e, cel aproximat azi prin 2,71828 și care a fost definit prima dată de Jacob Bernoulli abia în 1683, în contextul investigațiilor sale asupra compunerii dobînzilor. Notația cu litera e pentru baza logaritmilor naturali survine într-un manuscris rămas nepublicat în epocă al tînărului Leonhard Euler, din 1727 sau 1728, într-o lucrare care investiga forța de explozie a proiectilelor de tun. Anecdotica legată de acest număr ar putea include și așa-numita problemă a lui Steiner, care cere să se determine maximul funcției x la puterea 1/x. Acest maxim e atins exact la x = e.
E greu de imaginat că toate aceste dezvoltări ale matematicii moderne s-ar fi putut realiza dacă sistemul zecimal nu ar fi fost adoptat în plin Ev Mediu și dacă, după o evoluție de secole, toate aceste importante cîștiguri nu ar fi ajuns să edifice algebra așa cum o înțelegem azi. Arta de a calcula eficient e una dintre cele mai frumoase cuceriri ale umanității, iar dimensiunea umanistă a matematicilor include și povestea algebrei, de care se leagă atîtea dintre speranțele de altădată. Cu cît putem calcula mai bine, cu atît mai multă informație putem sistematiza, cu atît mai repede putem înțelege fenomene ale vieții reale și putem controla cît mai mult din realitatea noastră. De fapt, aceasta e miza cea mare: în zorii istoriei, destinul omului era subordonat capriciului elementelor. Speranța că putem calcula exact, grație tehnicii noastre, e legată de dorința de a controla cît mai mult posibil din lumea noastră.
Bogdan Suceavă este romancier, eseist, poet și matematician. Cea mai recentă carte a sa este Furtuna barocă, Polirom, 2024.
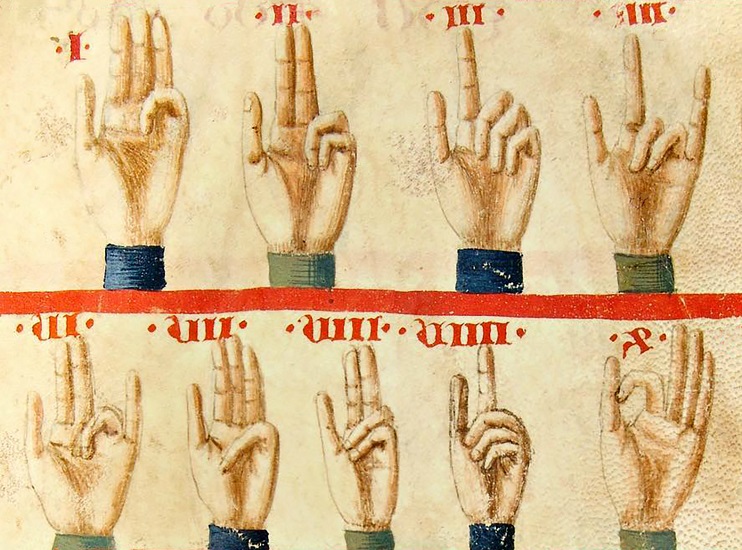
Foto: Liber abaci



















.jpg)







